Below are some "Discussion Sessions" to be used with students in conjunction with the book Struck by Lightning: The Curious World of Probabilities. Each Session consists of a short reading assignment from the book, together with some questions to inspire discussion. The intention is that the students will first do the reading and make notes about the questions on their own (e.g. as homework), and then the entire class will have a full discussion of the issues raised. (The students should also be invited to offer additional observations / comments / questions / opinions about the readings.) I have found that the Sessions lead to class discussions usually lasting approximately 45 minutes.

The book and questions are appropriate for group study or for high-school or university students. You are welcome to use these Discussion Sessions in your own teaching. If you do, I would appreciate your letting me know.

Below are also links to some "Supplementary Materials" (in pdf format) for in-class small-group exercises. They are listed under the chapter to which they most closely correspond, but many of them can be used at virtually any point in the course. Their levels and lengths vary, but generally they are slightly more mathematical/technical exercises which expand upon the book's material. They usually take about 45-60 minutes including follow-up discussion, and work well for groups of 3-4 students with limited mathematics background. (See also a related course and other questions.)

Discussion Session #1: Introduction

1. Make a brief point-form list of the 3-4 different kinds of randomness, mentioned in the chapter, that you found the most interesting (and why).
2. List 2-3 kinds of randomness (whether mentioned in the chapter or not) that have affected your life in some interesting way (and explain how).

Discussion Session #2: Coincidences, Part I

1. What does the book mean by "out of how many"?
2. Consider the following six "stories" from the reading: the lottery winner, the ten coin flips, Disney World, the friend's dream, Richard Feynman, the molecules of water, and Darth Vader versus Lord Dark Helmet. For each of these six stories:
   (a) Provide a one-sentence summary of the story.
   (b) Explain (in one more sentence) what we can conclude from the story.
3. Describe Milgram's "six degrees of separation" experiment. Had you heard of it before? Do you find it interesting? What can we learn from it? What flaws did it have?
4. What are "Erdos numbers"? What other similar "numbers" have been developed? Do you find them interesting? Can you suggest any other similar "numbers" not mentioned in the book?
5. Think of two or three "coincidences" that have occurred in your own life. For each one, answer the following questions:
   (a) Did you find it surprising? Why or why not?
   (b) Did you feel that it happened just by chance, or that it had some special significance? Why?
   (c) To what extent do you feel that it can or cannot be explained by considering "out of how many"?

Discussion Session #3: Coincidences, Part II

1. Why is it so much more likely that some pair of people at a party will have the same birthday, than that someone at the party will have their birthday today? Explain.
2. Do you think that some pair of people in this class has the same birthday? Why or why not? What if we also include everyone's mother's birthday, as well?
3. Why does the value 0.69 (on page 16) represent "a little bit of overcounting"?
4. How do you think we could calculate the exact probability that some pair out of 23 people has the same birthday? [Hint: This is equal to one minus the probability that no pair has the same birthday, i.e. that every birthday is different.]
5. What is the conclusion of the "Musical Mayhem" story? Do you find it surprising?
6. What is "Poisson clumping"? How is it related to Figure 2.1? How is it related to the five Toronto homicides in the first week of November, 2003? What other examples of Poisson clumping does the book allude to?
7. What is the "common cause" explanation? How does it relate to the "Parental Musings" story?
8. Think of at least two examples of coincidences from your own life, or that you have heard or read about, which you think can be explained by "number of pairs" or "Poisson clumping" or "common cause". Describe your reasoning.

Discussion Session #4: Law of Large Numbers, Part I

1. What are the "two key facts" which explain why casinos always make money? Did you already know these facts? Do you find them surprising?
2. What is the Law of Large Numbers, and how is it related to casino profits?
3. What can we conclude from the "Honorable Bus Fine" story?
4. What are all the different roulette bets which are considered?
5. For each of those bets, how is the average outcome calculated? What does it work out to be?
6. What "gambler's ruin" question is considered (p. 27)? What answer is provided? How does this answer compare with what you would have guessed? How difficult do you think it would be to compute this answer mathematically?
7. What can we conclude from the "Slowly but Surely" story?

Discussion Session #5: Law of Large Numbers, Part II

1. Summarise the three different explanations for why, when rolling two ordinary dice, the most likely sum is 7. Did you already know that fact? Do you find the explanations convincing?
2. Explain how to compute the probability of getting at least one 3, if you roll an ordinary die 4 times. And of getting at least one pair of 6's, if you roll a pair of ordinary dice 24 times. What is the historical significance of these calculations?
3. Explain the rules of craps, and the probability of winning.
4. Do you know (or can you easily figure out) how to compute the probability of winning at craps? If yes, explain how. Or, if no, explain why it is difficult, and whether or not you would like to learn how.
5. What is a "Don't Pass Line" bet? Why does it not give the edge to the player?
6. Summarise the examples presented in the section "A Life of Large Numbers". Do you find the asserted connections to the Law of Large Numbers to be convincing? Why or why not?
7. Come up with at least two examples from your own life, of events which are somehow related to the Law of Large Numbers.

Discussion Session #6: Card Games and Beyond

1. What is the point of the Larry Bird and bowling examples?
2. Do you play bridge? Poker? Other games of chance? Do you enjoy them?
3. In bridge, what is a "finesse"? How do expert players differ from novices when it comes to finesses?
4. What is duplicate bridge? To what extent does duplicate bridge eliminate luck from bridge? Explain. How is this related to the "Bridge Bickering" story?
5. In poker, what is the probability of successfully drawing to a Flush? How does this depend on the opponents' face-up cards?
6. What is the difference between drawing to an Inside Straight and an Outside Straight? How are the probabilities related? Why?
7. Explain the probability calculation in the "Showdown" story on page 50.
8. What are "pot odds"? How can they help make decisions when playing poker? Explain the pot odds calculation on page 51.
9. Why is "patience" required to be successful at games of chance? How is this related to the Portuguese Postal Puzzle story?
10. Think of at least two examples from your own life in which you had a high probability of winning or succeeding at something, but you still didn't win due to bad luck and insufficient repetition.

Discussion Session #7: Homicide Counts and Rates

1. According to the book, what segments of society declare that violent crime is increasing? What evidence does the book give for this?
2. Can you think of any other examples of people declaring that violent crime is increasing?
3. What is the difference between homicide counts, and homicide rates? Why is this distinction important?
4. Give at least four examples from the book of pairs of countries or regions, for which one of them has a higher homicide count, and the other one has a higher homicide rate.
5. What is the connection between homicide rates versus counts, and the "out of how many" principle from Chapter 2?
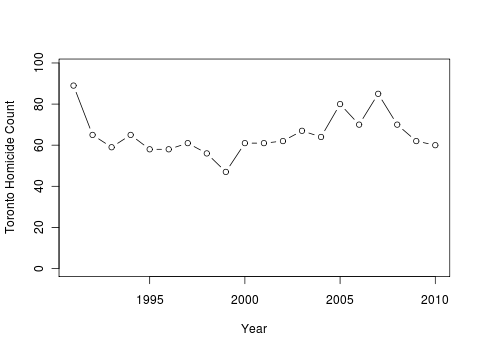
6. Describe the data in Figure 5.2, noting as many features as you can. What do you think we can and cannot conclude from this graph? Explain your reasoning.
7. In the summer of 2005 (just after the book was written), the city of Toronto experienced a higher-than-usual number of homicides involving handguns, leading to many alarming headlines ("summer of the gun", "Toronto has lost its innocence", "guns used to bathe Toronto in blood", ...). Do you feel that this was the start of a new and dangerous period of violent crime, or merely a statistical fluctuation that will soon disappear? Explain your reasoning. The following data may help:

   
   
   

   Homicides per 100,000 population of various metropolitan regions in 2005:

   Toronto 1.96; Winnipeg 3.72; Regina 3.97; Edmonton 4.29; New York 6.60; Los Angeles 12.6; Chicago 15.6; Buffalo 19.8; Detroit 39.5. All of Canada: 2.04. (Toronto in 1991: 2.41.)

Discussion Session #8: Homicide Trends

1. What is "regression", and how does it avoid bias and subjectivity? How does it relate to the "Weight Gain, Weight Loss" story?
2. Explain the purpose and conclusion of each of the first five figures of Chapter 5, i.e. Figures 5.1, 5.2, 5.3, 5.4, and 5.5. Also explain the relation between the different figures: do they present different information? are they all necessary? why or why not?
3. Summarise the comparison of homicides in the U.S., Canada, Australia, and Great Britain. Do you find any of the comparisons surprising? Why or why not?
4. Summarise the content of Table 5.3. Do you find any of the information surprising? Why or why not?
5. Summarise the comments about crime rate trends in the section "Playing with Numbers?" What is your reaction to these comments? Why does the section conclude by saying "Just the facts, ma'am"?
6. Last Session, we discussed the question of whether Toronto's higher-than-usual number of homicides in 2005 represented the start of a new and dangerous period of violent crime, or merely a statistical fluctuation that will soon disappear. Has your opinion on this question been affected by anything from this Session? Why or why not?

Discussion Session #9: Utility Functions

1. Summarise the two decisions made in the story "Walk or Ride?" Do you agree with the decisions? Why or why not?
2. What are utility functions?
3. How were utility functions used in the book to decide about the wedding, and about phoning "Juan"? (Explain the calculations used.)
4. Do you personally believe that expected values of utility functions are a good way to make decisions? Do you think that most people make decisions this way (whether they realise it or not)? Why or why not?
5. Summarise the calculations in the book about the insurance policy. Why does the book say that insurance can sometimes be a win-win situation? Do you personally believe in purchasing insurance? Why or why not?
6. Summarise the various examples of differing utility functions in the section "Your Utility or Mine?" Give an example from your own life where two people had significantly different utility functions, and a conflict that arose as a result.
7. On a scale where seeing a pretty good movie equals +10, decide (with brief explanation) on the value of your own personal utility function for each of the following events: (a) getting caught in the rain without a jacket; (b) finding a $20 bill; (c) losing a $20 bill; (d) winning one million dollars; (e) winning ten million dollars.
8. Based solely on your utility function values, would you be willing to run through the rain without a jacket (a) in order to pick up a $20 bill you found? (b) in order to pick up a lottery ticket that had one chance in a million of being worth ten million dollars? (Explain your calculations.)
9. Think of an example (as different as possible from those already mentioned in the book or the previous question) of an event which is quite unlikely, but which would have significant consequences. Give a rough guess of its probability, and also decide (with brief explanation) the value of your utility function for the consequences (again, on a scale where seeing a pretty good movie equals +10).

Discussion Session #10: Medical Studies, Part I

1. Summarise the "Lucky Shot?" story. What answer would you give to the boyfriend at the end?
2. What does it mean to "just get lucky"?
3. What are p-values? (Give as much detail as possible.)
4. What is the "5% standard"? Do you feel that 5% is an appropriate standard? Why or why not? Does it depend what is being studied?
5. Discuss the various calculations related to the Probabilitus example and the candies example.
6. In the Probabilitus example, suppose instead that 70 patients out of 100 were cured. Do you think this would this "prove" that the drug works? Why or why not? What mathematical quantity would be important for determining this?
7. What is the principle of "regression to the mean", why does it arise, and what examples does the book provide?
8. Explain "sampling bias" and "reporting bias". Summarise the book's examples of them. Think of two additional examples not from the book.
9. On July 31, 2005, the Globe and Mail newspaper's web site conducted an on-line survey, in which they asked, "Which medium do you rely on most to keep abreast of the news?" They received 1623 responses, and the results were: Television, 194 votes (12%); Radio, 110 votes (7%); Newspapers, 298 votes (18%); Internet, 1013 votes (62%); Magazines, 8 votes (0.5%). To what extent does this survey "prove" that most Canadians receive most of their news from the Internet? Explain. How is this related to medical studies?

Discussion Session #11: Medical Studies, Part II

1. What is "publication bias"?
2. Summarise the stories about each of: asking your mom/dad; Happiness Hats; Dr. Nancy Olivieri; Dr. Betty Dong; and Vioxx. What do these stories all have in common? What can we learn from them?
3. What did the International Committee of Medical Journal Editors declare in 2001? How is it related to publication bias? Do you feel that it will completely solve the problem of bias in medical studies? Why or why not?
4. What does it mean that "correlation does not imply causation"?
5. Summarise the stories about each of: the Jumping Frog; cigarettes and yellow stains; the Meditation Medical Miracle; the medical school class presidents; and television versus violence. What do these stories all have in common? What can we learn from them?
6. What are "randomized trials"? How do they relate to correlation and causation? Do you think they solve all problems of interpreting causation? Why or why not?
7. The next time your doctor tells you to take a certain drug or action because studies prove it is beneficial, how will you react? Why?

Optional Mid-Course Amusement:

Then, if you wish, make up your own humorous probability story -- just a few paragraphs long -- in the spirit of the book's Interlude. (You can later read your story out to the class.)

Discussion Session #12: Election Polls

1. What elections (including referenda) are referred to in these readings? (List as many as you can.) Which of them had you already heard of?
2. Why does the book claim that "polls provide us with more direct democracy than elections do"? To what extent do you agree or disagree? Why?
3. Why does the book claim that polls "provide an extra level of communication among the electorate"? What examples are given to support this claim? To what extent do you agree or disagree with it? Why?
4. According to the book, what does a poll's "margin of error" really mean? What factors does it take into account? What factors does it not take into account?
5. What examples does the book give of elections (and referenda) in which voter opinion changed after polls were conducted? (List as many as you can, and provide as much detail as possible.)
6. What examples does the book give of situations in which respondents will provide dishonest or misleading answers to pollsters?
7. Summarise the (fictional) story about the "Apathy Party", and explain what we can learn from it.
8. Explain the example of the cannabis survey, and how a "randomized response" poll could help.
9. Given everything you have learned so far about election polls, to what extent do you think they can or cannot be used to predict the results of an upcoming election? Explain.

Discussion Session #13: Margins of Error

1. From a probability perspective, in what way is conducting a poll like flipping coins? In what way is it different?
2. What does the book claim is the "95% Range for Percentage of Heads when Flipping 10 Coins"? What does this mean?
3. What about for 100 coins?
4. What formula does the book claim for the margin of error when flipping lots of coins? Do you understand how it was derived? How is it related to the "bell curve"? How is it related to the margin of error for polls?
5. For each of the four polls summarised on pages 145-146:
   (a) How closely does the published margin of error follow the claimed formula?
   (b) How close was the poll's result to the actual election result?
   (c) Was the poll's true error (compared to the actual election result) more or less than the published margin of error?
6. Find some election poll not mentioned in the book (e.g. from the internet, or from a current election), which includes the number of people sampled and a margin of error. How closely does the published margin of error match the book's formula?
7. What examples does the "Uncertain Day" story give about how margins of error might arise in everyday life? For each example, do you agree that it is a valid illustration of margins of error in everyday life? Why or why not?
8. Present at least two additional examples, not mentioned in the book, of how margins of error might arise in everyday life.

Discussion Session #14: Randomness to the Rescue

1. What action does the book claim gives results that the CIA couldn't reproduce in a million years? Do you believe this? Do you find it surprising? Why or why not? Does it give you any new perspective about your daily activities, and if so, what?
2. Give an additional example (not from the book) of types of things people frequently do, which have probably never occurred before precisely that way in all of human history.
3. Explain the stories of the million monkeys and the Internet searches. Had you heard of them before? Do you find them surprising? Why or why not?
4. Perform a few Internet searches of your own (on search strings not from the book), using the Google search engine, keeping track of the number of hits each time, to further illustrate the book's story about Internet searches. You could try random digits, random letters, or even random sequences of words (within quotation marks).
5. Explain the examples about Johnny Hooker, Rock/Paper/Scissors, and the World Series. Did you find them convincing? What do they all have in common?
6. Do you think that the game Rock/Paper/Scissors involves some skill, or is just pure luck? After considering this question, try out the NYT RPS robot (on "Veteran" mode); how did you do, and how does that affect your answer to this question?
7. Summarise the uses of randomness by computers. Do you find any of them surprising?
8. What are "pseudorandom numbers"?
9. Summarise the story "Dividing the Restaurant Bill". Do you feel that the solution reached was fair? Why or why not? How is the solution related to the Law of Large Numbers? How are these questions related to this auction house newspaper story?
10. Have you ever considered using such a method in the past? Would you consider using such a method in the future?

Discussion Session #15: Randomness in Biology

1. What did you previously know about the importance of probability in biology?
2. What rule does the book give for genes being passed from parent to child? How is this related to eye colour?
3. What does the book claim about children of two Light-eyed parents? Does this claim agree with your observations about yourself and/or your family and friends?
4. What does the book claim about children of one Light-eyed and one Dark-eyed parent? How about two Dark-eyed parents?
5. What does the book claim about the eye-colour genes of the book's author?
6. How is the spread of viruses related to probability?
7. Summarise the story "Spread the Word". How is it related to the spread of viruses?
8. What is "herd immunity"? How is it related to HIV/AIDS and to vaccines?
9. Summarise the history of the MMR vaccine in the United Kingdom. What can we learn from this story? (See also this update.)
10. What does the book say is the "total fertility rate" of the world? Of Canada? What is the significance of these figures?
11. Recently, Canada has had yearly totals of about 340,000 births, 230,000 deaths, 240,000 immigrants, and 40,000 emigrants. What does this say about Canada's population change in recent years? How is this related to the previous question?
12. What does the book mean by "self-replicating"? What self-replicating examples are given? What to they all have in common, related to probabilities?
13. What other sciences (besides biology) do you think are related to probability? In what ways?

Discussion Session #16: Conditional Probability and Spam

1. Summarise the (brief) stories about crossing the road, passing an examination, and "the woman of my dreams". What do they have in common?
2. Summarise the stories about each of the bearded men, the lupus scare, and the spelling bee. (Include details of the calculations made.) What can we learn from them?
3. What common societal situations/reactions are analogous to this "Beware the Bearded Men" story? (Think of as many as you can.)
4. What is spam e-mail?
5. Why does spam e-mail have that name? [See also the original Monty Python spam skit.]
6. What is automatic spam filtering?
7. What does the book describe as a "first attempt" at automatic spam filtering? How does it work? What are its limitations?
8. Summarise the stories "The Dastardly Spammity Spam" and "Spammity Spam Revisited". What can we learn from them?
9. Explain probability-based spam filters (giving as much detail as possible). Do you think they are more effective than previous spam filters? Why or why not?
10. Read the blog post "Adventures in spam, part two". How is it related to the above issues?
11. Does your own personal e-mail account have a spam filter (e.g., a "junk folder")? Approximately how many spam messages per week does it catch? How many does it miss? Do the spam messages ever contain intentionally misspelled words like "Vi@gra"?

Discussion Session #17: Causes of Randomness

1. What does the book mean when it says that randomness is often based on ignorance?
2. Summarise the story of the Restless Restauranteur, and relate it to the previous question.
3. How does the book explain the randomness of flipping a coin?
4. What does it mean for a system to be chaotic? (Give as much detail as possible.)
5. What examples of chaotic systems does the book give? (List as many as you can, and discuss whether or not you agree that they are chaotic.)
6. What are some other examples, not mentioned in the book, of chaotic systems? Of non-chaotic systems? (Try to think of at least two of each.)
7. Do you agree with the book's assertion that "meteorologists are ambassadors of probability"? Why or why not?
8. Do you often listen to weather forecasts? If yes, then how do you feel about them? Do you think they are usually accurate? Do they describe probabilities in a way that you find clear?
9. Are you surprised that probability theory is related to physics? Why or why not?
10. What does the theory of quantum mechanics say about nature and randomness? (Give as much detail as you can.)
11. How are chaos and quantum mechanics related to the random numbers used by computers? (Provide as many connections as you can.)
12. Do you believe that nature is truly random? Why or why not? If yes, then does this affect your perception and feelings about the universe, and if so how?

Optional End-of-Course Amusement:

Then, as a group, come up with at least three additional "Final Exam" style questions about this course, in a similar style to those in the book (i.e. multiple choice, obvious answer, humorous, etc.). (You will later read some of your questions out loud to the entire class.)

The book Struck by Lightning, by Jeffrey S. Rosenthal, may be ordered from e.g. amazon.ca (or in paperback) or indigo.ca (or in paperback) or amazon.com or amazon.co.uk or barnesandnoble.com, or from many bookstores. See also the Struck by Lightning main page.