MARGINS OF ERROR IN OPINION POLLS

Jeffrey S. Rosenthal, 2003

Note: Margins of error are discussed in a more accessible way in my 2005 book Struck by Lightning: The Curious World of Probabilities. See also an UPDATED VERSION OF THIS ARTICLE (August 2018).

Suppose you flip a coin ten thousand times. How many heads will you get? On each flip, the coin has equal probability of coming up heads or tails. So, on AVERAGE, you will get five thousand heads and five thousand tails. On the other hand, it doesn't seem likely that you will get EXACTLY five thousand heads -- rather, you will get "about" five thousand heads. But how much UNCERTAINTY is there around that mean value? That is, how far off from five thousand can we expect it to be? Might you get six thousand heads? Seven thousand? Or will you usually get between 4995 and 5005?

Meanwhile, we are constantly bombarded by the results of opinion polls. For example, in October, 2002, the polling firm Environics did a poll of political preferences in the Province of Ontario. They surveyed four hundred adult residents, and reported what fraction would support each of several political parties if there were a provincial election. They then boldly proclaimed that "The margin of error for a sample of 400 is approximately plus or minus five percentage points, 19 times out of 20." In another poll they surveyed one thousand adults, and declared that their results were "estimated to be accurate within 3.1 percentage points, 19 times out of 20." Similar claims are made all the time. What in the world do they mean? And, how can the polling firms be so sure?

It turns out that these two questions, about coins and polls, are pretty much the same question. And they both involve the same three concepts: the mean (or average value), the standard deviation (the amount of uncertainty), and the normal distribution (or bell-shaped curve).

MEAN AND STANDARD DEVIATION

First consider flipping just one coin. Half the time it will come up heads, and half the time tails. Thus, on average you will get one-half of one head. Of course, in actuality you will never get one-half of a head -- you will get either zero or one heads. But still, the AVERAGE number of heads you will get is one-half. We express this mathematically by saying that, if you flip a coin, then the "mean" number of heads is one-half.

Now, when you flip that coin, you will always be off from the mean (one-half) by exactly one-half (since zero heads is off from one-half by one-half, and one head is also off from one-half by one-half). So if you flip one coin, the number of heads will differ from its mean by one-half.

Mathematically, the amount you tend to be off from the mean is called the "standard deviation". So, if you flip one coin, then the mean number of heads is one-half, and the standard deviation of the number of heads is also one-half. That is, on average you will get one-half of one head, but on average you will also be off from this amount by one-half.

The question now is, suppose you flip ten thousand coins. What will be the mean (average value) and the standard deviation (amount you tend to be off from the average value) of the number of heads then?

Well, the mean is easy. We already know that on average you will get five thousand heads. Put another way, the mean is equal to the mean for one coin (i.e., one-half), multiplied by the total number of coins (ten thousand). That is:

mean = (1/2) x (10,000) = 5,000

It turns out that the standard deviation increases by multiplying by only the SQUARE-ROOT of the number of coins. (Remember that the square-root of 4 is 2, since 2 x 2 = 4; the square-root of 9 is 3, since 3 x 3 = 9; the square-root of 100 is 10, since 10 x 10 = 100; and the square-root of ten thousand is one hundred, since 100 x 100 = 10,000. In general, the square-root of a number is the quantity that, when multiplied by itself, equals the number.) This is the key fact to understanding uncertainties. Namely, if you do any repeated experiment (like flipping coins) many times, then the amount of uncertainty is multiplied by only the square-root of the number of experiments performed.

How can we make use of this fact? Well, we know that if you flip one coin, the mean number of heads is 1/2, and the standard deviation is also 1/2. So, if you flip four coins, then the mean number of heads is 1/2 times 4, which equals 2 (of course); but the standard deviation is just 1/2 times the SQUARE-ROOT of 4, which equals 1/2 times 2, which is 1. That is, if you flip four coins, then on average you will get two heads, but you will tend to be off from this average value by about 1 in either direction -- that is, you might get one or three heads instead. (Of course, you MIGHT get zero or four heads as well, and be off by 2. Or, you might get exactly two heads, and not be off at all. But ON AVERAGE you will be off from two heads by about 1 in either direction.)

Now that we understand this principle, we can extend it to any number of coins. If you flip one hundred coins, the mean number of heads is 1/2 times 100, which is 50; and the standard deviation is 1/2 times the square-root of 100, which is 1/2 times 10, i.e. 5, so on average you will be off from the mean value of 50 by about 5 heads either way. Finally, if you flip ten thousand coins, then the mean number of heads is 1/2 times 10,000, which equals 5,000; and the standard deviation is 1/2 times the square-root of 10,000, which is 1/2 times 100, i.e. 50. That is:

standard deviation = (1/2) x SquareRoot(10,000) = (1/2) x 100 = 50

Notice that as you flip more and more coins, the amount you tend to be "off" from the mean value increases, but quite slowly, so that even after 10,000 coin flips, you tend to be "off" from the mean value (5,000) by just 50. The rest of the uncertainty from those ten thousand individual coin flips has canceled out, with the extra heads balancing off the extra tails until just a relatively small amount of uncertainty remains.

So, now that we know about the mean and standard deviation, how can we figure out the margins of error used by polling firms? To understand that better, we need to examine the bell-shaped curve.

THE BELL-SHAPED CURVE (NORMAL DISTRIBUTION)

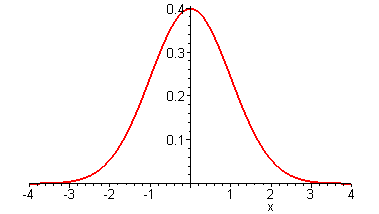
You may have seen the famous bell-shaped curve at one time or another. It is a beautiful graph, higher in the middle, and drifting down in a lovely arc on either side. It turns out that this elegant curve is closely related to flipping lots of coins -- and to conducting an opinion poll of lots of residents.

The connection is given by what mathematicians call the "Central Limit Theorem". This remarkable theorem was first discovered by the French mathematician Abraham de Moivre way back in 1733, and was refined over the following century by his compatriot Pierre-Simon Laplace and by the German mathematical legend Johann Carl Friedrich Gauss. (In fact, the theorem is so important that generalisations and extensions of it still form an active area of mathematical research even today.)

The Central Limit Theorem says that, if you repeat a bunch of random actions (like flipping lots of coins), and add up the outcomes (like counting the total number of heads), then the resulting probabilities will follow the bell-shaped curve (also called the "normal distribution"). Specifically, the probability that the result will be within one standard deviation of its mean value, is equal to the area under the bell-shaped curve between -1 and +1. Similarly, the probability that the result will be within three standard deviations of its mean value, is equal to the area under the bell-shaped curve between -3 and +3. And so on.

What this means is as follows. Suppose you you flip ten thousand coins, and wonder what is the probability that the actual number of heads will be within one standard deviation (i.e. fifty), either way, of its mean value (five thousand). That is, what is the probability that you will get between 4950 and 5050 heads? The answer is that this probability is equal to the area under the bell-shaped curve between -1 and +1. We can measure that this area is about 0.68, i.e. 68%.

In other words, the number of heads will be between 4950 and 5050 about 68% of the time. So, if you repeat this experiment one hundred times -- each time flipping ten thousand coins and counting the number of heads -- then in about sixty-eight of the one hundred experiments, the number of heads will be between 4950 and 5050, while in the other thirty-two experiments the number of heads will be either less than 4950, or more than 5050.

If we wanted to announce this, we might say: "If you flip ten thousand coins, then 68 times out of 100, the number of heads will be between 4950 and 5050." Or, "If you flip ten thousand coins, then 68 times out of 100, the number of heads will be within 50 (either way) of five thousand." Or, "If you flip ten thousand coins, then the number of heads will be within 50 of its true mean, 68 times out of 100." Or, "If you flip ten thousand coins, then the margin of error is plus or minus 50, 68 times out of 100." These statements are all true, and all mean the same thing.

Similarly, in this case THREE standard deviations is equal to three times fifty, or 150. And being within 150 of its mean corresponds to getting between 4850 and 5150 heads. So, the probability of this is equal to the area under the bell-shaped curve between -3 and +3. We can measure that this area is about 0.997, i.e. 99.7%, which corresponds to 997 times in a thousand. So, it is a virtual certainty (happening 99.7% of the time) that the number of heads will be within 4850 and 5150.

Now, we might think that "68 times out of 100" is not often enough to give us a sufficient sense of certainty. We might equally well think that "997 times out of a thousand" is too often, and gives us more certainty than we will ever need. So how should we compromise? In fact, it is a tradition in statistics to find a range which will contain the number of heads 95 times out of 100, i.e. 95% of the time -- which is the same as "19 times out of 20". How can we find such a range?

Well, let's look again at the bell-shaped curve. As we take wider and wider ranges, we get more and more of the probability. In fact, we can measure that the area under the curve between -1.96 and +1.96 is equal to just exactly 0.95, corresponding to just exactly 95%, i.e. 95 times out of 100, i.e. 19 times out of 20. This says that, 95 times out of 100, the number of heads will be off from the mean by less than 1.96 times the standard deviation.

Now, if we flip ten thousand coins, then the standard deviation is 50. And, 1.96 times 50 equals 98. So, we should consider the probability that the number of heads will be within 1.96 times 50 of its mean, i.e. within 98 of its mean, i.e. between 4902 and 5098. According to the bell-shaped curve, this probability is equal to 0.95, i.e. about 95%, which equals 19 times in 20. So, if you again repeat this experiment one hundred times -- each time flipping ten thousand coins and counting the number of heads -- then in about ninety-five of the one hundred experiments, the number of heads will be between 4902 and 5098, while in the other five experiments the number of heads will be either less than 4902, or more than 5098. Alternatively, if you repeated this experiment just twenty times -- again, each time flipping ten thousand coins and counting the number of heads -- then in about nineteen of the twenty experiments, the number of heads would be between 4902 and 5098, while in the other one experiment the number of heads would be either less than 4902, or more than 5098.

We could announce this by saying: "If you flip ten thousand coins, then 95 times out of 100, the number of heads will be within 98 of five thousand." Or, "If you flip ten thousand coins, then the margin of error is plus or minus 98, 95 times out of 100." Or, "If you flip ten thousand coins, then the margin of error is plus or minus 98, 19 times out of 20." Again, these statements are all true, and all mean the same thing.

What if we wanted even greater certainty, say 99 times out of 100? Once again we look at the bell-shaped curve. We can measure that the area under the curve between -2.57 and +2.57 is equal to 0.99, i.e. to 99%, i.e. to 99 times out of 100. So, we are interested in 2.57 times the standard deviation, i.e. 2.57 times 50. Now, 2.57 times 50 equals 128.5; call it 128 (since we can never have .5 of a head anyway). So, we should consider the probability that the number of heads will be within 2.57 times 50 of its mean, i.e. within 128 of its mean, i.e. between 4872 and 5128. According to the bell-shaped curve, this probability is equal to 0.99, i.e. 99%. So, if you again repeat this experiment one hundred times -- each time flipping ten thousand coins and counting the number of heads -- then in about ninety-nine of the one hundred experiments, the number of heads will be between 4872 and 5128, while in the other one experiment the number of heads will be either less than 4872, or more than 5128. We could announce this by saying: "If you flip ten thousand coins, then 99 times out of 100, the number of heads will be within 128 of five thousand." Or, "If you flip ten thousand coins, then the margin of error is plus or minus 128, 99 times out of 100."

So, we see that if you flip ten thousand coins, then 99 times out of 100, you will be within 128 of the mean, i.e. you will get no more than 5128 heads. In fact, your chance of getting more than, say, six thousand heads is unfathomably small -- about one chance in the (huge) number written as a one followed by eighty-nine zeroes! So, you will never in your lifetime get as many as six thousand or more heads out of ten thousand. The mean number will be five thousand, and there just isn't enough uncertainty to ever increase the head count as high as six thousand. In real life, real coins just don't come up heads that often.

POLLING: WHO WILL WIN THE ELECTION?

We now return, finally, to polling, and the claim that "The margin of error for a sample of 400 is approximately plus or minus five percentage points, 19 times out of 20." We are now, finally, in a position to understand this claim.

Let us first understand what the claim does NOT mean. The polling firm is NOT claiming that, 19 times out of 20, they will predict the results of the next election with the specified accuracy. Such a claim would require a precise understanding of how political opinions change between the poll date and the election date; the extent to which citizens will say one thing to pollsters and then vote differently; the future actions of the "undecided" voters and those who did not respond to the survey; which citizens will or will not bother to vote; and a host of other intangible factors. Pundits and analysts do in fact work overtime trying to understand these factors, and statistical modeling can indeed be used to try to estimate them. But such issues are very complicated and subtle, and polling firms do not routinely make claims about their precise predictive powers in these areas.

No, what the polling firm is claiming is something far more mundane. They are claiming that the probability is about 19 out of 20 that their poll has uncovered the "right" answer, to within the specified accuracy. That is, if they immediately repeated the same experiment -- i.e. surveying four hundred residents' political preferences -- twenty different times, then about nineteen of those times, they would get the "right" answer to within the specified accuracy. But here the "right" answer means simply the fraction of all the adult residents throughout the province, who would claim support for a particular political party, when phoned by a pollster at that particular time. In other words, the polling firm's claim provides reassurances that the polling firm has done its job, and that they have sampled enough residents that the poll results have a certain meaning, but only in so far as determining what the general population currently feels like telling pesky pollsters on the phone.

With this clarification out of the way, we can now ask, where does a figure like "plus or minus five percentage points" come from? How does the polling firm compute their claimed accuracy?

The key to answering this is to observe that polling random residents is much like flipping coins. In each case, you are repeatedly conducting a random experiment (flipping a coin, or polling a resident), and counting the number of times you get a specified result (i.e. a head, or professed support for a particular political party). So, we can use our knowledge of uncertainty in coin flipping, to understand the uncertainty in a political poll.

When flipping four hundred coins, the mean number of heads is two hundred (of course). Also, the standard deviation is equal to one-half times the square-root of 400, i.e. one-half times 20, which equals ten. What about when polling four hundred residents?

Well, in this case the mean is the average number of residents, in a random sample of four hundred people from the province, who support the particular political party. This is, in fact, precisely what the polling firm is trying to figure out! So, in this case we do not know what the mean is at all. It is not equal to two hundred (like for coins), but rather is some unknown value.

On the other hand, the standard deviation is just the same as when flipping four hundred coins, since each poll response introduces randomness just as each coin flip does. So, the standard deviation is still equal to ten! Even though we no longer know the mean, we still know the standard deviation. (In fact, it can be argued that the standard deviation is actually a bit LESS than ten, especially for political parties whose support is in fact quite small. But it is never MORE than ten, so we can use the figure of ten without worry -- and in fact this is what polling firms usually do.)

Now, for flipping four hundred coins, since the standard deviation is ten, we know that 68 times out of 100, the number of heads will be within ten of the true mean. Also, 1.96 times the standard deviation equals 1.96 times ten, or 19.6. So, 95 times out of 100, the number of heads will be within 19 of the mean. Finally, 2.57 times the standard deviation equals 2.57 times ten, or 25.7. So, 99 times out of 100, the number of heads will be within 25 of the mean.

The remarkable thing is, these facts are still true when polling four hundred residents! The mean is now different (and unknown), but the probabilities are still the SAME for how far OFF from the mean we will be. So, if you survey four hundred residents, then 68 times out of 100, the number claiming support for a particular political party will be within ten of the true mean; And, 95 times out of 100, it will be within 19 of the mean. And, 99 times out of 100, it will be within 25 of the mean.

But the polling firm doesn't report the NUMBER of adults in their survey who supported each party, they report the FRACTION. That is, they divide the number supporting each party, by four hundred (the total number of adults surveyed). So, if the number is within 10 of the true mean, then the FRACTION is within 10 divided by 400 of the FRACTION'S true mean (i.e., of the fraction of the general population supporting that political party). But 10 divided by 400 equals 10/400, or 0.025, or 2.5%. So, 68 times out of 100, the FRACTION of residents claiming to support a particular party will be within 2.5% of the true fraction of the general population claiming support for that that party. Hence, if we surveyed four hundred adults, and announced the fraction of our survey sample supporting each political party, then we could announce that, "68 times out of 100, our results will be accurate to within 2.5% of the true value". Or even, "The margin of error of our results is plus or minus 2.5 percentage points, 68 times out of 100."

Similarly, we know that 95 times out of 100, the number of surveyed residents supporting a particular party will be within 19 of the true number, meaning that the fraction will be within 19/400, or 4.75%, of the fraction's true mean. Hence, we could also announce that, "95 times out of 100, our results will be accurate to within 4.75% of the true value". Or, "19 times out of 20, our results will be accurate to within 4.75% of the true value", which is the same thing. Or even, "The margin of error of our results is plus or minus 4.75 percentage points, 19 times out of 20." Or to avoid the extra decimal places, we could say, "The margin of error of our results is approximately plus or minus five percentage points, 19 times out of 20." Now we sound just like the polling firm!

What about the other poll, which surveyed one thousand residents? Well, in this case the standard deviation (of the number of replies for each political party) is equal to one-half times the square-root of one thousand. The square-root of one thousand is about 31.6, so the standard deviation is one-half times 31.6, which equals 15.8. So, when surveying one thousand adults and counting the number who support some particular political party, then 68 times out of 100 the number will be within 15 of the true mean. Also, 1.96 times the standard deviation is 1.96 times 15.8, which is about 31. So, 95 times out of 100 the number will be within 31 of the true mean. Finally, 2.57 times the standard deviation equals 2.57 times 15.8, which is about 41. So, 99 times out of 100 the number will be within 41 of the true mean. This gives the probabilities for how far off will be the NUMBER of residents supporting each party.

To consider the FRACTION of residents supporting each party, we have to divide by the total number of residents surveyed, in this case one thousand. Now, 15.8 divided by one thousand equals about 1.6%, while 31 divided by one thousand equals about 3.1%, and 41 divided by one thousand equals about 4.1%. So, for this poll, we could announce that "68 times out of 100, our results will be accurate to within 1.6% of the true value". Or, "95 times out of 100, our results will be accurate to within 3.1% of the true value". Or, "99 times out of 100, our results will be accurate to within 4.1% of the true value". Or, "our margin of error is 3.1%, 95 times out of 100". Or, "our margin of error is 3.1%, 19 times out of 20". Or, as the polling firm puts it, our results are "estimated to be accurate within 3.1 percentage points, 19 times out of 20."

Other polls can be handled similarly. Indeed, the next time you read a poll, you can figure out the margin of error for yourself!

Note that if you survey MORE people (say, one thousand instead of four hundred), then the margin of error for the fraction of people supporting various political parties gets SMALLER (in this case, 3.1% instead of 4.75%). This is not surprising. It says essentially that the more people you ask, the more you know. In fact, this observation is what mathematicians call the "Law of Large Numbers". Namely, the more times you try an experiment -- like flipping coins or polling residents -- the closer your fractions get to their true mean values.

Once we understand mean, standard deviation, and the bell-shaped curve, we can now quantify many different types of uncertainty and margin of error in mathematical terms. Whether flipping coins or conducting polls, we know what the average value will be, and how far off from that average value we will usually be. Such information is crucial for determining the accuracy of polls, the reliability of medicines, the risks of stock purchases, and many other uncertainties which confront us on a daily basis.

Note added later: This model for polling assumes that the people selected for the poll are chosen uniformly at random from the entire population, with replacement (i.e., the model allows for the possibility that the same individual would be chosen twice in the same poll). Of course, in a real poll one doesn't ask the same person twice (or at least tries not to). So, one difference between this model and a real poll is whether the sampling of the population is done with or without replacement. When the number of people polled is much smaller than the full population (the usual case), this difference is unimportant. But hypothetically, if nearly the entire population were polled, then this difference would become important.

-- Jeffrey Rosenthal / Struck by Lightning / contact me